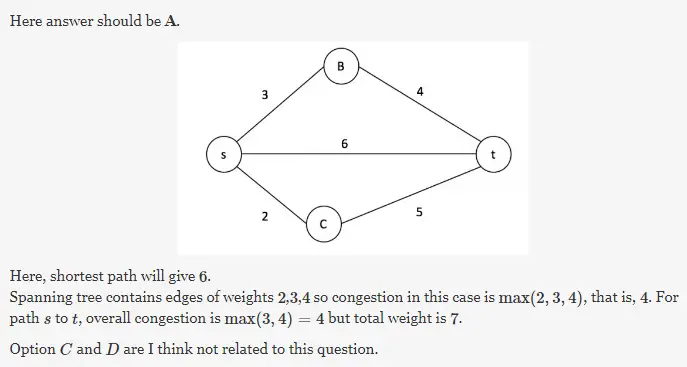
Q. 84 Let s and t be two vertices in a undirected graph G + (V, E) having distinct positive edge weights. Let [X, Y] be a partition of V such that s ∈ X and t ∈ Y. Consider the edge e having the minimum weight amongst all those edges that have one vertex in X and one vertex in Y.
Let the weight of an edge e denote the congestion on that edge. The congestion on a path is defined to be the maximum of the congestions on the edges of the path. We wish to find the path from s to t having minimum congestion. Which one of the following paths is always such a path of minimum congestion?
(A) a path from s to t in the minimum weighted spanning tree
(B) a weighted shortest path from s to t
(C) an Euler walk from s to t
(D) a Hamiltonian path from s to t
Answer: (A)
Explanation: